Using Python to Simulate Brownian Motion

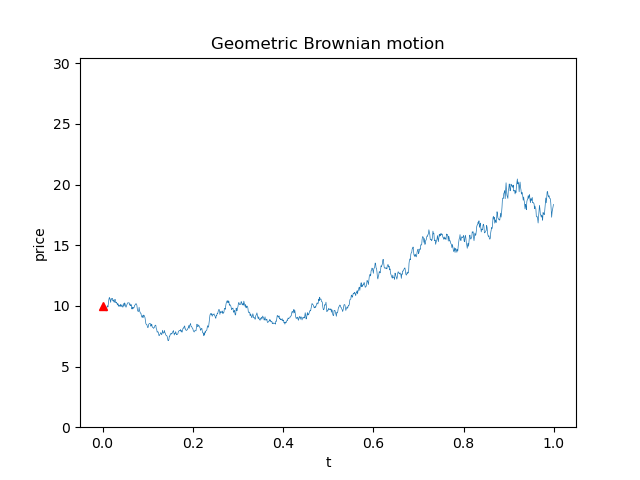
Brownian motion is a phenomenon that particles in the seemingly motionless liquid are still undergone unceasing collisions in an erratic way. It was firstly observed by Robert Brown in 1827. In 1923, Norbert Wiener had attempted to formulate this observations in mathematical terms; thus it is also known as Wiener process.

Owing to its randomness, Brownian motion has a wide range of applications, ranging from chaotic oscillations to stock market fluctuations. In this article, I will describe its basic property and how to visualise it and its variants with Python.

The Model of Brownian Motion

To begin with, we should see how to make Brownian motion in a rather formal way.

We firstly consider one dimensional coordinate system for simplicity. Imagine that you put a particle at the origin (\(x = 0\)) in the very beginning, and it may encounter random collisions along the \(x\)-coordinate afterwards. Let \(X(t)\) be the position of the particle after \(t\) units of time (\(X(0) = 0\)).

When the particle is undergone some collisions, we say there are events occurred. From physical obervations, scientists find that the probability of events occurred in any two equal time intervals, say \([s, t]\) and \([s+h, t+h]\), are not only equal but also indepedent. In other words, they have the same probability distribution, and no matter how many events occurred in \([s, t]\), it would not affect the number of events occurred over \([s+h, t+h]\). This can be represented as

\[ X(t) - X(s) \sim X(t+h) - X(s+h) \]

Actually, such property that they possess stationary and independent increments are usually called stationary increments. This is the bedrock of Brownian motion.

Thus, if $ t_1- t_0 = t_2-t_1 = t_3-t_2 = t_4-t_3 = $ ... ,

\[ X(t_1)-X(t_0) \sim X(t_2)-X(t_1) \sim X(t_3)-X(t_2) \sim X(t_4)-X(t_3) \dots \tag{1} \]

For \(t>s>0\), we tend to assume increments are normal distribution:

\[ X(t+s) - X(s) \sim \mathcal{N} (0, \sigma^2 t) \tag{2}\]

If $ \sigma = 1, $ it is also known as a standard Brownian motion, $ W(t) $.

It is worth noting that the path of Brownian motion is everywhere continuous but nowhere differentiable.

Visualise the Brownian Motion

Now we are ready to draw our Brownian motion in Python.

Some Toolkits

Below are the modules we will use to draw our plots.

from math import sqrt, exp
from random import random, gauss
import numpy as np
import matplotlib.pyplot as plt

Visualisation

As shown in \((1)\) and \((2),\) the increments between any equal time interval share the same Gaussian distribution. We are able to compute \(X(t)\) iteratively, i.e.

$$ \displaylines { X(t_1) \sim X(t_0) + \mathcal{N} (0, dt \cdot \sigma^2) \\ X(t_2) \sim X(t_1) + \mathcal{N} (0, dt \cdot \sigma^2) \\ X(t_3) \sim X(t_2) + \mathcal{N} (0, dt \cdot \sigma^2) \\ \dots } $$

, where $ dt = t_1-t_0 = t_2-t_1 = t_3-t_2 = $ ... .

mean = 0
std = random()  # standard deviation

N = 1000    # generate N points
dt = 1/N    # time interval = [0,1]

data = []
x = 0
for t in range(N):
    dx = gauss(mean, std*sqrt(dt))  # gauss(mean, standard deviation)
    x = x + dx                      # compute X(t) incrementally
    data.append((dt*t, x+dx))

data = np.array(data)

plt.figure()
plt.plot(data[:, 0], data[:, 1], linewidth=0.5)
plt.scatter(data[0, 0], data[0, 1],marker="^",color='r',label="Origin")
plt.xlabel('t')
plt.ylabel('x')
plt.legend()
plt.title("Brownian motion")
plt.show()

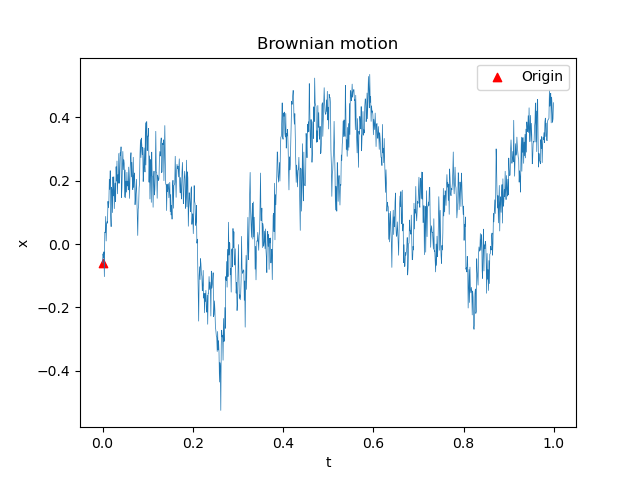
2D-Brownian Motion

Similarly, if we extend our coordinate system to two dimensions,

$$ \displaylines { X(t_1) \sim X(t_0) + \mathcal{N} (0, dt \cdot \sigma^2) \; \; \; \; \; Y(t_1) \sim Y(t_0) + \mathcal{N} (0, dt \cdot \sigma^2) \\ X(t_2) \sim X(t_1) + \mathcal{N} (0, dt \cdot \sigma^2) \; \; \; \; \; Y(t_2) \sim Y(t_1) + \mathcal{N} (0, dt \cdot \sigma^2) \\ X(t_3) \sim X(t_2) + \mathcal{N} (0, dt \cdot \sigma^2) \; \; \; \; \; Y(t_3) \sim Y(t_2) + \mathcal{N} (0, dt \cdot \sigma^2) \\ \dots } $$

, where $ dt = t_1-t_0 = t_2-t_1 = t_3-t_2 = $ ... .

mean = 0
std = random()

N = 1000    # generate N points
dt = 1/N    # time interval = [0,1]

data = []
x, y = 0, 0
for t in range(N):
    dx = gauss(mean, std*sqrt(dt))
    dy = gauss(mean, std*sqrt(dt))
    x, y = x+dx, y+dy
    data.append((x, y))

data = np.array(data)

plt.figure()
plt.plot(data[:, 0], data[:, 1], linewidth=0.5)
plt.scatter(data[0, 0], data[0, 1],marker="^",color='r',label="Origin")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title("2D-Brownian motion")
plt.show()

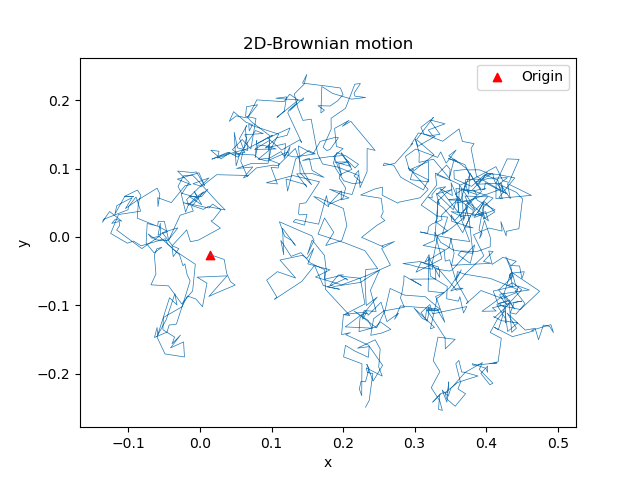
3D-Brownian Motion

The Brownian motion over 3-dim coordinate system is also trivial when you grasp the idea.

mean = 0
std = random()  # standard deviation

N = 1000    # generate N points
dt = 1/N    # time interval = [0,1]

data = []
x, y, z = 0, 0, 0
for t in range(N):
    dx = gauss(mean, std*sqrt(dt))
    dy = gauss(mean, std*sqrt(dt))
    dz = gauss(mean, std*sqrt(dt))
    x, y, z = x+dx, y+dy, z+dz
    data.append((x, y, z))

data = np.array(data)

plt.figure()
ax = plt.axes(projection='3d')
ax.plot3D(data[:, 0], data[:, 1], data[:, 2], linewidth=0.5)
ax.plot3D(data[0, 0], data[0, 1], data[0, 2], marker='^', color='r')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('3D-Brownian motion')
plt.show()

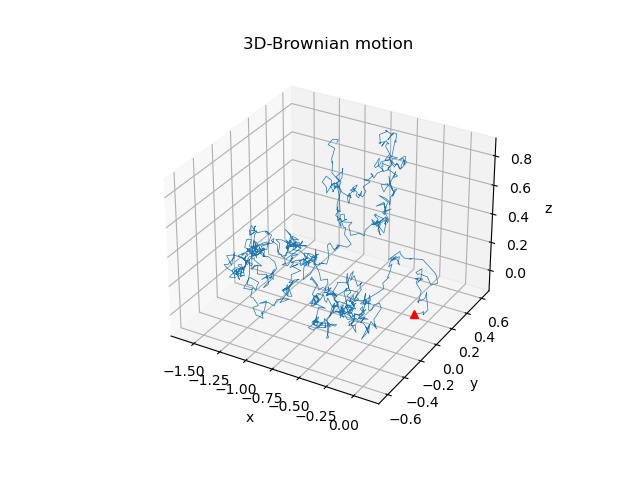
Geometric Brownian Motion

In finance, random fluctuations are quite common in stock prices or other derivatives and assets. To build the mathematical model upon the Brownian motion, we need to make a few tweaks because such prices would never be negative. A simple approach to tackling this is that we could assume the trend follows exponential growth or decay curves in the long run:

\[ S(t) = s_0 \cdot e^{X(t)} = s_0 \cdot e^{\mu t + \sigma W(t)} \]

, where \(S(t)\) is the stock price at time \(t\) and \(s_0\) is the initial price. We use $ X(t) = \mu t + \sigma W(t) $ with drift parameter \(\mu\) and \(W(t)\) : the standard Brownian motion. Clearly, $ S(0) = s_0 $. The drift parameter can decide the trend for this model, whereas \(\sigma\) implies the degree of unpredictability. This type of process is usually called exponential Brownian motion or geometric Brownian motion.

The Relationship between Stock Prices at Time \(t\)

As the model is established, we can observe the increments now lies in the ratio change

\[ \frac{S(t_i)}{S(t_{i-1})} = e^{\mu(t_i - t_{i-1})} \cdot e^{\sigma [W(t_i) - W(t_{i-1}) ] } \]

Therefore,

\[ \frac{S(t_1)}{S(t_0)} \sim \frac{S(t_2)}{S(t_1)} \sim \frac{S(t_3)}{S(t_2)} \dots \]

, where $ dt = t_1-t_0 = t_2-t_1 = t_3-t_2 = $ ... .

Below are a simple simulation of stock prices over the trading days in a year, with its initial at $10.

mean = random()
std = random()

N = 253     # trading days in a year
dt = 1/N

x = 10.0    # initial stock price
data = [(0, x)]
for t in range(1, N):
    ratio = exp(mean*dt) * exp(std * gauss(0, sqrt(dt)))
    x = x * ratio
    data.append((dt*t, x))

data = np.array(data)

plt.figure()
plt.plot(data[:, 0], data[:, 1], linewidth=0.5)
plt.plot(data[0, 0], data[0, 1], marker='^', color='r')
plt.xlabel('t')
plt.ylabel('price')
plt.ylim([0, max(data[:,1]+10)])
plt.title("Geometric Brownian motion")
plt.show()