East TechNote

Perhaps it's all about Math

0%

Sampling - Inverse Transformation Method

Posted on Edited on In ,

Sometimes, we may wanna simulate certain random variable to get the desired approximation. Yet, if the scenario is rather complicated, the computation cost can be exorbitant. With the help of inverse transformation method, we are able to generate many special random variables efficienctly.

A Toy Example

With replacement, we draw cards at random from an ordinary deck of 52 cards, and successively until an ACE is drawn. What is the probability of exactly 10 draws?

Apparently, let \(X\) be the number of draws until the first ace. The random variable \(X\) is of geometric distribution with the parameter \(p = \frac{1}{13}\). The answer of the desired probability is

\[ P(x) = (1-p)^{x-1} * p = (\frac{12}{13})^9 * (\frac{1}{13}) \]

Simulating \(X\)

Now, if we wanna approximate the desired probability by simulating \(X\), an intuitive way might look like as below:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
### Pseudo-code of Simulation

i = 0    # iterator
k = 0    # Record the desired events
while i < N:      # Repeat N trials
    draws = 0     # Count how many draws when the first ACE appears
    while True:   # Draw the card with replacement until it is an ACE
        draws +=1
        Generate a random sample x from [A,2,3,4,...9,10,J,Q,K]
        if x is ACE:   # Let 1 represent the ACE
            break

    if draws is 10:  # Number of draws is exactly 10
        k +=1
    
    i +=1

prob = k/N   # The approximate value

From the experiment, it can be observed that \(N\) has to be quite large (>10000) if we would like to get enough accuracy:

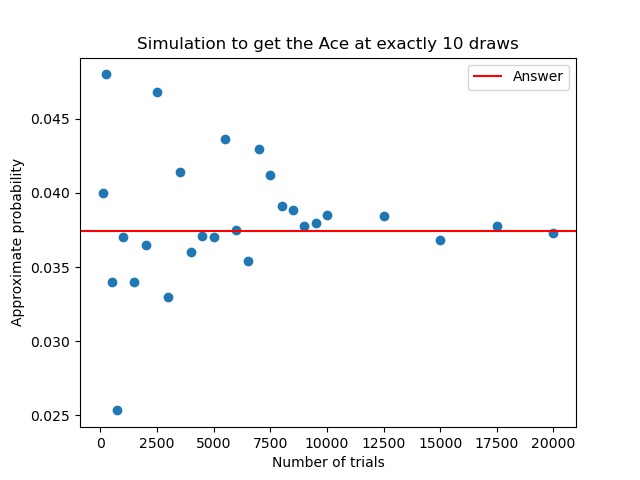
Below is the source code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt

# N trials
# k: Count the desired events obtained in N trials

N = [100, 250, 500, 750, 
     1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000,
     5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500,
     10000, 12500, 15000, 17500, 20000]
approx = []

for n in N:
    i = 0
    k = 0
    while i < n:
        # draw the card with replacement until it is ACE
        j = 0
        while True:
            j +=1
            draw = np.random.randint(1, 13)
            if draw == 1:
                break

        if j == 10:  # draw number is 10
            k +=1
        
        i +=1

    approx.append(k/n)

ans = (12/13)**9 * (1/13)

plt.scatter(x=N, y=approx)
plt.xlabel('Number of trials')
plt.ylabel('Approximate probability')
plt.axhline(y=ans, color='r', linestyle='-', label='Answer')
plt.legend()
plt.title('Simulation to get the Ace at exactly 10 draws')
plt.show()

However, this approach is not efficient because the time complexity is proportional to the draw number. Thus, let's introduce the inverse transformation method. By this method, we are able to get the same result as well but only need to choose one random point in (0,1), significantly reducing the time cost.

Inverse Transformation Method

Let \(F(X) = P(X \leq x)\) be the probability distribution function of the random variable \(X\). Remember that for uniform random variable \(U\) over \((0,1)\),

\[ F(U) = P(U \leq x) = x, x \in (0,1) \tag{1} \]

Imagine that our objective is to simulate a random variable \(X\) from a uniform random variable \(U\), i.e., \(P(X \leq x) = P(T(U) \leq x)\). We hope to find a transformation \(T\) that is able to convert the random variable \(U\) into our desired \(X\).

$$ \displaylines { P(X \leq x) \\ = P(T(U) \leq x) \\ = P(U \leq T^{-1}(x)) \\ } $$

Remember that \(F(X) = P(X \leq x)\) and from \((1)\):

$$ \displaylines { P(U \leq T^{-1}(x)) \\ = P(U \leq F(x)) \\ = P(F^{-1}(U) \leq x) } $$

\[ \longrightarrow X = F^{-1}(U) \tag{2} \]

From \((2)\), we know the transformation \(T\) we are looking for is just \(F^{-1}\). Therefore, after solving \(F^{-1}\), we are able to generate the desired \(X\) from uniform random variable \(U\) directly without complications.1

Simulating Geometric Distribution via Inverse Transformation Method

Back to our original problem, we wanna simulate \(X\) in the toy example, and we know that the \(F(x)\) of geometric distribution with parameter \(p\) is

\[ F(x) = 1 - (1-p)^{x-1} \]

Solve \(u = F(x)\):

$$ \displaylines { u = 1 - (1-p)^{x-1} \\ x = 1 + \frac{\log{(1-u)}}{\log{(1-p)}} } $$

\[ \equiv 1 + \frac{\log{u}}{\log{(1-p)}} \tag{3} \]

If \(u\) is a random number variable from (0,1), then \((1-u)\) is a random number variable from (0,1) as well.

Now, from \((3)\), we are able to generate \(X\) from \(U\) efficiently. Because \(X\) is an integer, we use the floor operation (with the ceiling is also equivalent):

\[ X = \lfloor 1 + \frac{\log{u}}{\log{(1-p)}} \rfloor \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
### Pseudo-code of Geometric Distribution Simulation with Inverse Transform method

i = 0    # iterator
k = 0    # Record the desired events
while i < N:      # Repeat N trials
    Generate a uniform random variable u from (0,1)
    # p is the parameter of geometric distribution
    X = floor(1 + log(u)/log(1-p))   # inverse transform
    if X is 10:
        k +=1

    i +=1

prob = k/N   # The approximate value

Below is the experimental result and the related source code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
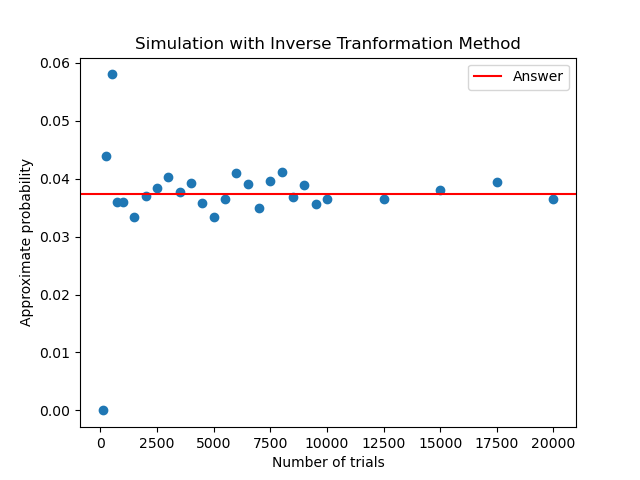
37
import numpy as np
import matplotlib.pyplot as plt
from math import log, floor

# N trials
# k: Count the desired events obtained in N trials

N = [100, 250, 500, 750, 
     1000, 1500, 2000, 2500, 3000, 3500, 4000, 4500, 5000,
     5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500,
     10000, 12500, 15000, 17500, 20000]
approx = []
p = 1/13

for n in N:
    i = 0
    k = 0
    while i < n:
        # inverse transformation method
        u = np.random.rand()
        X = floor(1 + log(u)/log(1-p))
        if X == 10:
            k +=1
        
        i +=1

    approx.append(k/n)

ans = (12/13)**9 * (1/13)

plt.scatter(x=N, y=approx)
plt.xlabel('Number of trials')
plt.ylabel('Approximate probability')
plt.axhline(y=ans, color='r', linestyle='-', label='Answer')
plt.legend()
plt.title('Simulation with Inverse Tranformation Method')
plt.show()

Performance Comparison

Let N be 500000 trials.

Original method:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
### Original Method
from time import perf_counter

i = 0
k = 0

t1_start = perf_counter()
while i < 500000:
    # draw the card with replacement until it is ACE
    j = 0
    while True:
        j +=1
        draw = np.random.randint(1, 13)
        if draw == 1:
            break

    if j == 10:  # draw number is 10
        k +=1

    i +=1
t1_stop = perf_counter()

print("Elapsed time (sec):", t1_stop-t1_start)

Inverse transformation method:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from time import perf_counter

i = 0
k = 0

t1_start = perf_counter()  
while i < 500000:
    # inverse transformation method
    u = np.random.rand()
    X = floor(1 + log(u)/log(1-p))
    if X == 10:
        k +=1
    
    i +=1
t1_stop = perf_counter()

print("Elapsed time (sec):", t1_stop-t1_start)

Results:

N = 500000 (trials) Elapsed Time (sec)
Original Method 10.832
Inverse Transformation Method 0.363

We can observe that the elapsed time has been substantially reduced after applying inverse transformation method.

Note that the inverse transformation method is to mainly improve the computation cost. It does not increase the convergence rate. From the previous experimental results, you can see that the N trials required to converge are roughly the same for both methods.

  1. For rigorous proof, you can refer to Inverse transform sampling. The aim here is to grasp the idea intuitively.↩︎